Databases
From Suhrid.net Wiki
Jump to navigationJump to searchContents
Relational Databases
- Set of named relations (tables)
- Each relation has a set of named attributes (columns)
- Each tuple (row) has a value for each attribute
- Each attribute has a type (or domain)
- All queries return relations (tables), so it can said to be compositional or closed.
XML Data
- Alternative to relational model to store data
- Standard for data representation and exchange
- Document format similar to HTML, however tags represent content instead of formatting.
- XML consists of tagged elements which can be nested, attributes of elements and the text (values/data)
- XML document can be thought of as a tree with values/text forming the leaves.
Relational vs XML
| Relational | XML | |
|---|---|---|
| Structure | Tables | Hierarchical/Tree |
| Schema | Fixed in advance | Flexible, self-describing. e.g. all elements need not have same attributes. (In relational, we would need to have NULL values). Inconsistencies in the structure is NOT a problem. |
| Queries | Relatively simple | Complicated compared to Relational / SQL. |
| Ordering | Fundamentally UNORDERED. e.g. Order by clause is required in SQL in case order is desired. | Ordering is implied - e.g. the way the text is laid out in the XML document or in the Stream. |
| Implementation | Mature - native implementation | Add - on. (Underlying implementation is relational) |
Well formed XML
- Single root element
- XML parser is used to validate XML.
- DOM parser - treats XML as a document, SAX parser - treats XML as a stream.
- Matched tags, proper nesting
- Unique attributes within each element
Displaying XML
- Since XML occurs a lot on the internet, a convenient way is required to display XML.
- Use rule based languages such as CSS, XSL to translate XML to HTML.
- XML document is fed to a CSS/XSL interpreter alongwith rules and a HTML document is generated.
Valid XML
- Valid XML should adhere to requirements for well formed XML
- Also should adhere to content-specific specifications : DTD/XSD
- DTD is a grammar-like language for specifying elements, attributes, nesting, ordering, #occurrences
- DTD/XSD offers the benefits of "typing" - can serve as a specification. Useful for data exchange.
- Having no DTD offers flexibility of data.
- DTD also can specify pointer types - an element can have an ID and another element can refer to it using an IDREF.
XSD
- Like DTD, but more comprehensive.
- XSD is written in XML itself.
- Everything in DTD is string, in XSD e.g., we can specify that an attribute should be of a specific type.
- Pointers can be typed, so we can enforce that a reference is made to a particular type and not just global like in DTD's
- Also specify min/max constraints on elements
JSON
- Like XML, JSON can be thought of as a data model - as an alternative to the relational data model.
- Useful for semi-structured data
- Designed originally for serializing data objects
- JSON is human readable - often used for data interchange
- JSON consists of base values, objects (label-value pairs), and arrays to hold either. Structure is recursive.
- JSON vs Relational - JSON differs in how data is stored, schema is self-describing, ordering is present, query support is minimal unlike XQuery, XPath, XSLT, and is implemented typically in prog languages
- JSON vs XML - XML more verbose/complex than JSON, like DTD, XSD, JSON has JSON schema.
- XML model dont match with programming languages. Interface is clunky. This is called impedence mismatch - similar to Relational and prog languages.
- JSON has a more direct mapping with prog languages.
Valid JSON
- Adheres to basic structural requirements of JSON. (label-value pairs, arrays of values)
- Can use JSON schema for semantic validation.
Relational Algebra
- Relational algebra is the formal language that is the underpinning for implemented languages like SQL
- Query (expression) on a set of results produces relation as a result.
- Simplest query in RA is the name of the relation e.g. Student which produce the contents of the Student relation
- Operators to filter, slice and combine relations.
- Select operator : Sigma (cond) Relation name. Condition is a filter and the result will be a subset of the relation
- Project operator : Select picks rows, project picks columns. Pi (col name) Relation Name.
- To pick both rows and cols, combine the select and project operator. e.g. Project(sid,name) (Select(gpa > 3.7) student)
- Cross Product : By default RA is based on sets and doesnt consider duplicates. But SQL uses multisets/bags and includes duplicates - Cross product between two relations combines all attributes (columns) and every combination of tuples between the relation. m X n attrs and a X B tuples.
- Natural Join : Is like cross product but enforces equality on all attributes with the same name. Eliminate one copy of duplicate attributes (same attribute from diff table). So if we use the nat. join operator we dont need to specify the key attributes need to be equal condition. Doesnt provide any additional expressive power, but is convenient notationally.
- Theta Join : A convenience like natural join. Basically apply the theta condition to the cross product of two relations. This is the "join" that is implemented in most DBMS.
- Union operator : Used to produce a list.
- Difference operator : Here but not there.
- Intersection : Both here and there.
- Rename operator : Necessary to express certain queries. Takes a result of a schema and calls it something. This name can be used later on. Useful for unifying schemas for set operators (Relational Algebra) rule and for disambiguations in self-joins (joins on the same relation).
SQL
- Two parts - DDL (create,drop) DML (query and modify)
- SQL is declarative - what, not how. Therefore, query optimizer is very important.
- Selecting from multiple tables is a join, but unlike relational algebra, we need to specify the join condition manually.
- e.g. select a from person, city where person.lives = city.name
- SQL essentially follows an unordered model.
- Order on multiple cols can be specified. e.g order by age, population - age will be sorted and population will be sorted for a given age.
- Like RA, SQL has set operators.
- Union : Union eliminates duplicates, Union all includes duplicates
- Intersect : Some DB's dont support it, but can be simulated using join
- Except : (Set Difference). Again some db's dont support it.
- Subqueries : Useful for counting duplicates instead of join. Join can eliminate some required duplicates etc - The In clause comes in play. To simulate except - in A and not in B
- In uses to check whether values exist in the subquery or not. Exists can be used to check whether the result of the subquery is empty or not.
- Subqueries can refer to variables in the main query.
- Exists can be used to find largest/smallest. e.g. select name from student s1 where not exists (select * from student s2 where s2.gpa > s1.gpa) - all students such that there does not exist another student who's GPA is higher
- Any & all operator can be used to qualify a subclass. Any/all can be equally expressed using the exists clause.
- Subqueries can be used in the FORM and SELECT clauses apart from the WHERE clause. A sub query in the from clause allows you to write a select from where expression
and then use the result of that expression as if it were an actual table in the database. Subqueries in SELECT clause must just return one value.
- Null values in DB can produce unexpected results - distinct does include null, but count of distinct does NOT. Watch out.
Aggregation
- Perform computations over sets of values in multiple rows. Basic aggregation functions : min, max, avg, count. Part of select clause.
- With aggregate functions, we get two new clauses - group by and having. Group by allows to partition our relation into groups and will compute aggregate functions over group independently.
- Having allows to filter on the results of aggregate values. "where" applies to a single row, "having" applies to the groups that are generated in the group by clause
- count(*) also allows count(some col) - we can also do count(distinct col) which can be quite useful
- "Group by" is used only in conjunction with aggregation. - Grouping takes a table and partitions it by values of a given attribute or a set of attributes. e.g. group by sName will partition student according to names. select count(*) from Student group by sname - counts of groups of students eaching having the same name.
- A query with group by/having can be rewritten as a complicated query without those clauses.
Modification
- Insert into table values OR
- Insert into table (Select statement) : result of the select will be inserted into the table
- Delete from table (condition) : condition can be a subquery : but some db systems dont fully support this where the subquery references the same table
- Update table set attr = expre where condition, (need not have a where clause also)
Join
- In from clause when we list multiple tables, it is implicitly a cross product of the tables.
- Inner join on condition : Equivalent to theta join in RA. Cross product with a condition. Default join operator. So "inner" keyword is not necessary. e.g. select x from a join b on a.someid = b.otherid
- Natural join : Elimnates duplicates in columns with the same name. Therefore, no need to specify "on" clause. select sName from student natural join apply
- Inner join with Using clause (using specific attributes) : This is better practice than using natural join to actually specify the attribute to join on.
- Outer join : left / right / full. To add tuples that dont match the join condition. outer can be left out. So only left join is ok.
- Left : any tuples on the left with no matching tuple on right will be added. Outer join can also be written as a natural join if the using clause is not specified.
- Right : vice-versa
- Full : unmatched tuples from both left & right. Basically it is a left outer join UNION right outer join
- Note: the outer join is NOT associative. A ojoin (B ojoin C) <> (A ojoin B) ojoin C
- Join ordering offers hint to SQL query executor on how to execute joins. So tweaking join ordering can be used to influence query performance.
Relational Design Theory
- Design anomalies
- Redundancy : Duplicate information
- Update anomaly : Direct effect of redundancy. Update facts in some places but NOT ALL. Or update differently in different places - we end up with an inconsistent database.
- Deletion anomaly : Allowing a complete deletion about something. e.g. if surfing is a hobby and stored alongwith student, if we delete surfing, then we delete those students whose only hobby is surfing.
- The best design for a relational DB, depends not only about constructing the relations well, but also on what the data is representing in the real world.
- Design by decomposition
- Start with mega relations that contain everything
- Decompose into smaller relations with same info
- Automatic decomposition can be done - "Mega" relations + properties
- System uses properties of the data to perform decomposition.
- Final set of relations satisfies a normal form - i.e. no anomalies present and NO lost data.
- Functional dependencies - System generates Boyce Codd Normal Form
- FD + Multivalued dependencies - Fourth Normal Form.
- A functional dependency A -> B, means A functionally determines B. e.g. SSN -> Name. An SSN always maps to the same name, but not necessarily the other way around. This relationship should be stored once.
It is a 1-1 mapping. There can be only 1 B value given an A.
- What BCNF says is that when we have a functional dependency, the left side of the FD (i.e. A) must be a KEY.
- Multi-valued dependencies : A ->> B. Take the relation Apply(ssn, cname, hs) : This is in BCNF, becaue there are no FD's. But there is redundancy, for every cname, hs, we'll have c*h tuples.
There is a MVD from SSN to CName, and HS. SSN->>CName, SSN->>HS. i.e. have every combination of those two attributes and values in those attributes for a given social security number. cname and HS are essentially independent. So store them once. So 4NF says if A->>B, then A should be a key. So Apply(ssn, cname, hs) can be decomposed into Apply(ssn, cname) and HighSchool(ssn, hs). So we get c+h tuples rather than c*h tuples.
Functional Dependencies
- FD's are a generalization of the notion of keys.
- FD's apart from being used in relational design are also useful in data storage : generating compression schemes and for query optimization.
- example of FD. Two rows with same value of ssn have same name. For all t, u E Relation if t.ssn = u.ssn => t.name = u.name. (ssn -> name)
- So in general, A -> B. It can be extended to a set of attributes A1, A2, ... AN -> B1, B2 ... BM
- If a row1 has values A1 AND A2 then row2 will have values B1 AND B2.
- A, B -> C. Unique combination of A & B will have a unique value of C.
- A' -> all attributes. Set of attributes in A' determines all other attributes, then the set of attributes in A' can said to be a key.
- A -> B. Trivial FD : B is a subset of A, Nontrivial FD : B is not a subset of A, Completely nontrivial FD, A intersect B is empty. This is what we are interested in capturing.
- Splitting rule : A' -> B', then we can say A' -> B1, A' -> B2 etc. But we cannot say A1 -> B', A2 -> B'. Splitting is allowed only on the RHS.
- Combining rule : Inverse of splitting rule.
- Trivial FD rule : if A -> B, then A -> A U B & A -> A Intersect B.
- A -> B, B -> C, then A -> C.
- Closure of attributes : Given a relation R, FD's and a set of attributes A', find all B such that A' -> B. B is called the closure of A.
- Algo : start with the set A', keep adding RHS of FD's to the set, until we are done with all FD's.
- If a set of attributes determines all attributes in the relation, than that attribute is the KEY for the relation. So a closure is a tool to find out the keys for a relation.
- Is A' a key for R ? Compute A+ , if A+ consists of all attributes in the relation, then A' is a key for the relation R.
- Given a set of FD's, can we find keys ? Yes, compute closure of subsets in increasing order, whenever we find a subset whose closure is all attrs, then that subset and all its supersets is the key.
- Specifying FD's for a relation : S1, S2 are sets of FDs. S2, follows S1, if every relation instance satisfying S1 also satisfies S2.
- S1 : SSN -> GPA, GPA -> Priority : S2 : SSN -> Priority. S2 follows from S1.
- How to test in general ? S1 follows from S ? Test every FD in the set S1. Take a single FD to start : Does A' -> B' follow from S. Take closure of A' on S, if B' is in the closure then A' -> B' follows from S.
- Armstrong's axioms
- In the end, we want a minimal set of completely nontrivial FDs such that all FDs that hold on the relation follow from the dependencies in this set. i.e. Design Goal.
Boyce Codd Normal Form
- Decomposition of a relation schema R (A') into R1 (B') and R2 (C'). B' U C' = A' and R1 NatJoin R2 = R.
- Decomposition should be good decompositions - that is retain original attributes and the natural join of the decomposed relation should produce the original relation - called a lossless join. Also the decomposed relations must themselves be good.
- Relation R with FD's is said to be in BCNF, if for each A' -> B, A is a KEY. or contains a key - because the superset of a key is also a key.
- A relation R can have multiple keys - i.e. combo of attributes together act as key - and determine all other attributes. So to check if a relation is in BCNF, ask if the LHS of every FD is the KEY ? (multiple attributes combo).
- Given a set of FD's. Compute the closure of LHS of FD's. If it yields all attributes then its is a key. Like that every FD, needs to have a key on the LHS.
- "Good" relations are those that are in BCNF. "Good" decompositions is the process to arrive at good relations.
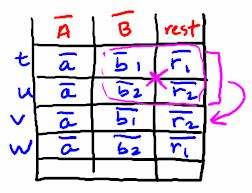
- BCNF Decomposition Algorithm
- Input : Relation R with FD's
- Output : decomposition of R into BCNF relations with lossless joins.
- Compute keys for R using FD's
- Repeat until all relations are in BCNF
- Pick any R' with A -> B that violates BCNF. i.e. A is NOT a key. Now decompose R into R1(A, B) and R2 (A, Rest)
- Compute FD's for R1, R2
- Compute Keys for R1, R2
Multivalued dependencies
- FD + MVD = 4NF. 4NF is stronger than BCNF, Any relation that is in 4NF also conforms to BCNF.
- Separation of independent facts is what 4NF is all about.
- A ->> B. If there are tuples, t u and v in R. Then if t[A] = u[A], then there exists a third tuple v such that v[B] = t[B] and v[rest] = u[rest]
- If A ->> B, we must have every combination of B and C (rest) values for A. Therefore, MVD's are called tuple-generating dependencies. Because it is about having additional tuples when we have existing tuples unlike FD's which talk about relationships among existing tuples.
- Example with values
- SSN ->> cName, then SSN ->> Hobby
- Suppose we define a MVD ssn, cname, date ->> major. What this is saying is that the major for a given ssn, cname and date varies independently from the rest - e.g. hobby.
- Different majors for same student, college, date. And the hobby can be anything else.
- SSN ->> cName,date says that (cName,date) and major are independent, i.e., all combinations of cName,date and major (i.e. "the rest") must be present for any college or major a student applies for.
- Start with the two given tuples. Try to apply the given MVDs to any pair of tuples you can (i.e., any pair of tuples that have the same values for the attributes on the left side of the MVD). Each application of an MVD lets you add two tuples to the relation: the tuples formed by swapping the values for the attributes on the right side of the MVD. (You may wish to review the formal definition of an MVD.) Repeat this process until all of the tuples implied by the MVDs are already in the relation.
- Rules:
- If we have an FD A -> B, then we also have an MVD A ->> B
- Trivial FD : If A ->> B, then B subset A or A U B is all attributes
- Nontrivial FD : Other than trivial FD.
- Intersection rule : A ->> B, A ->>C, then A ->> B intersect C
- Transitivity : A ->> B, B ->> C, then A ->> C - B
Fourth Normal Form
- Relation R with MVD's is in 4NF if for each nontrivial A ->> B, A is a key
- This means that since A is a key - there will NOT be a combination of the attributes of b and the rest that get generated.
- 4NF implies BCNF.
- Algo to find 4NF is similar to BCNF, except we use MVD's. FD's are used to find keys.
Summary
- R(ABC) : If A -> B , then when we have same A values we have same B values. BCNF tells us to move A, B into a separate relation.
- R (ABCD) : If A ->> B, then for every combination for a given A of B values and CD values. We take A & B attributes and put them in a separate relation so that they can remain independent from A & CD relationship.
Shortcoming of BCNF and 4NF
- When queries use many attributes, its better to store all such attributes in one relation even if it means redundant storage. To avoid combining data using joins.
- i.e. Store denormalized data rather than normalized.
- All dependencies may not be captured
- Query workload can be high
- Over decomposition
UML for Data Modeling
- Data modeling subset of UML can be used to model the data. Translator then converts it into relations.
- Every class becomes a relation. The PK attribute becomes the primary key. Other attributes are columns in the relation.
- Associations : UML association is also created a table and the pk attribute from each side of the UML association is added as columns.
- What will be the key for the association table ? If multiplicity on LHS is 0..1 & RHS is *. This means that one attribute on RHS is related to at most one attribute on the LHS. This means the PK from the right side is the key for the association.
- Also we may not need relations for associations at all. Suppose LHS has 1..1 and RHS is *. This means that every element in R2 is related to exactly one element in R1. So we can put R1's key as part of R2 rather than create a separate association relation. The key for R2 will still be K2 as from the previous point.
- In summary, the key for association will be from the opposite of 0..1 or 1..1. Or the opposite relation can contain the key rather then a separate association class.
- Association classes : Adds extra information to an association. Add these attributes to the relation created from the association class.
- Subclasses Properties
- Complete - each objects in superclass belong to one or more subclasses vs Incomplete (not the case) - in the superclass, but not in the sub.
- Disjoint (exclusive) - No object is in more than one subclass vs Overlapping (not the case)
- Consider superclass Student, with subclass Foreign & Domestic & AdvancedStudent.
- Foreign & Domestic are complete and disjoint, only AdvancedStudent is incomplete (can have students who are not Advanced), All three are complete and overlapping ( a student can be domestic and advanced).
Subclasses into relations
- Superclass S with K as PK and attr A, Subclass S1 with attr B, Subclass S2 with attr C.
- Three different ways this can be translated into relations.
- Subclass contains superclass key plus some additional attributes : Generate a relation for each class, with subclass relations containing the superclass key. This will require joins to get all attributes for a subclass.
- Subclass relation contains all attributes : Relation for each class. So no joins required.
- One relation containing all superclass and subclass attributes. Nulls may be present. e.g. for object from S1 it will have a null value of C.
- But best translation will depend on the properties of the subclasses.
- Suppose we have heavily overlapping subclasses - many objects that are in multiple subclasses - we may prefer design 3.
- In case of disjoint, we prefer design 2. If also complete, we can get rid of the Superclass relation itself.
- Else, probably design 1.
- Translation 3 has one tuple for each object regardless of subclassing. Translation 2 has one tuple for each object, plus one more each time an object is in more than one subclass. Translation 1 has one tuple for each object, plus one more for each time an object is in a subclass.
Composition & Aggregation
- Composition says that we have objects who are components of another object. e.g. Department is a component of College.
- Here we dont create a separate relation for the composition association. (1..1) But the component contains the key of its container. So Dept relation will contain PK of college.
- Aggregation is like composition, but the component need not belong to any container. If it does, just max of one container. (0..1). So for relations, it is same as composition, except that container key (PK of college) can be null in the component relation.
Indexes
- Primary way of getting improved performance from a Database.
- Persistent data structure stored in the DB.
- Index provides immediate access to tuples rather than full table scans. Also not only provide location of a value but can answer conditional questions as well.
- Underlying data structures : Balanced Trees : B/B+ Trees : useful for Attribute = Value; Attribute < Value, Attribute between two Values. Operations tend to be algorithmic in their running time.
- Hash tables : Can only be used for equality conditions. Operations will have constant running time.
- Many DB's automatically build indexes on Primary Key's and sometimes UNIQUE attributes.
- Indexes are also useful in JOINS. Say that one side of the join is indexed, then using the value from the unindexed side, index can quickly find the attribute on the indexed side.
- Multi column indexes : e.g create index on (col1, col2, col3) will help when all three cols are queries together as opposed to individual indexes on each column.
- Disadvantages:
- Take up extra space : Not that big a deal considering disk space is cheap
- Index creation : medium. Can take up a significant time, but worth it.
- Index maintenance: When values in DB change, index has to be modified. So in a DB that's modified often but not queries enough, the cost of index maintenance can offset the benefits of having an index.
- Picking indexes to create. Factors :
- Size of table
- Data distributions
- Query vs update load
- Physical design advisor : Takes an input of the DB (Statistics) and workload (sets of queries/updates & frequencies). Gives an output of recommended set of indexes.
- Relies on the query optimizer : Design advisor experiments with different sets of indexes and gives the own with least cost.
Transactions
- Motivated by two independent concerns : Concurrent access & System resilience
- Attribute level inconsistency : same attr updated, Tuple level inconsistency : diff attributes, same tuple
- Table level inconsistency : different tables but one query refers table1 using table 2, query 2 modifies table 2
- Multi statement inconsistency : query 1 : insert/delete some tables, query 2 : counting those tables
- So concurrency goal : Execute SQL statements in such a way so that they appear to be running in isolation
- System resilience : e.g. running a bulk load, but during that disk fails.
- System failure goal : Guarantee all-or-nothing execution, regardless of failures
- Solution for both concurrency & failures is transaction
- Each transaction is a sequence of SQL ops that is treated as a unit. Transactions appear to run in isolation, if system fails, each transaction's charges are reflected either entirely or not at all.
- In SQL, transaction begins automatically on first SQL statement and ends when commit is issued.
- Autocommit : each statement is a transaction
Transaction Properties
- ACID properties
- Isolation : Implemented by a formal notion called serializability. i.e Operations may be interleaved among transactions, but execution must be equivalent to some serial order of all transactions. e.g., T1, T2, etc. Operations among them can be intereleaved, but there should be a guarantee that in the end some serial order is maintained (in effect). e.g. T1, T3, T9, T2. Suppose Client1 issues T1, T2 & Client2 issues T3, T4 then any order like T1; T3; T2; T4 or T1; T3; T4; T2 etc.
- Durability : Guarantee that if the system crashes after transaction commits, all effects of transaction remain in Database.
- Atomicity : Crash during the transaction before commit. Atomicity guarantees that the transaction is ALL or NOTHING.
- DB introduced transaction rollback or abort to maintain Atomicity. However, rollback can be client initiated as well. Also, dont hold open transactions for long - since locking will be in place & other operations may be blocked.
- Consistency : Each client, transaction can assume all DB integrity constraints hold when transactions begin, & clients must guarantee that those constraints hold when the transaction ends. Since we have serializability of transactions, it is guaranteed that constraints always hold.
Isolation Levels
- Serializability provides understandable behaviour and consistency but has overhead in locking protocols & reduces concurrency.
- Therefore systems offer weaker isolation levels compared to "serializable". Default iso. level is serializable. Reduce overhead & increase concurrency but at some cost to consistency. Listed in order from weaker to stronger :
- Read uncommitted, Read committed and Repeatable read
- Isolation level is per transaction, so client can different isolation level for each of its transactions.
- Isolation level is "in the eye of the beholder". So C1 can have read uncommitted & C2 can have repeatable read & they will be guaranteed per transaction.
- Isolation levels are specific to reads
- Dirty item is one that has been written by a transaction but not yet committed. A dirty read is when a dirty item is read that was modified by a different transaction.
- Read uncommitted : Transaction may perform dirty reads.
- Read committed: NO Dirty Reads. Only read committed values. Still does not guarantee serializability. e.g. T1 updates some value, T2 has two statements that use T1's committed value, but S1 can execute before T1 commit & T2 can execute after commit.
- Repeatable read : A transaction may not perform dirty reads AND an item read multiple times cannot change value. Still does not guarantee global serializability. Because multiple items may not be read at all as in the above example - and serializability is not maintained. Oracle & MySQL have this set by default.
- However phenomenon known as "phantom tuples" can be prevented. Suppose T2 is repeatable read and has two statements reading some value. T1 is inserting that value. So both statements of T2, S1 & S2 are actually not reading different values but new "phantom" ones are being inserted. However, suppose T1 is deleting - then the delete/second read wont be allowed when T2 is running because the values are locked.
- Transactions can also be read only : Helps system optimize performance and is independent of the isolation level.
Constraints
- Known as integrity constraints as they constrain the allowable states of the database
- A static concept
- Schema imposes structural and type constraints. However, we need semantic constraints i.e. from the application level, e.g 0 <= GPA <= 4.0
- Constraints help :
- Catch data entry errors. (inserts)
- Correctness criteria. (updates)
- Enforce consistency.
- Tell the system about the data. e.g. key constraints. To make system more efficient in processing queries.
- Types : non-null, key, referential integrity (foreign key), attribute based - constraining the value, tuple - based : across attributes, general assertions (across tables)
- Constraints can be created alongwith schema. Constraints are checked after bulk loading.
- Or can be declared later : Constraint is checked on the current state when it is declared
- Enforcement : Everytime the data is modified
- Deferred constraint checking : During bulk modification, constraints may be violated but later should be OK. So check after transaction.
- If constraint is violated, DB will raise an error and undo the modification.
Integrity Constraints
- Primary key - there can only be one in a table. Has the purpose of identifying the row. Values should not be null (most systems) & should ideally not change.
- Unique key - can be many declared. Value can change.
- Primary key/Unqiue key can span several attributes, e.g create table(cname text, state text, enrollment int, primary key(cname, state)).
Attribute based constraints
- create table student (sid int, sname text, GPA real, check (GPA <=4.0 and GPA > 0.0), sizeHS int check (sizeHS < 5000))
- Checked whenever attr is inserted/updated
Tuple based constraints
- checked whenever tuples is inserted/updated, allows to check relationships based on different values in tuple
- create table student (sid int, sname text, GPA real, check (sid > 100 and GPA <= 4.0)
General assertions
- Many assertions are in the SQL standard but not supported by any systems. e.g. subqueries in attribute assertions
- General assertions are also not supported as of now.
- Assertions generally check for bad condition and assert that they do not exist. (like Java asserts)
Referential Constraints
- Specify no dangling pointers
- if we have a referential integrity from R.A -> S.B it means that each value of column A of table R must appear in column B of table S.
- Referential integrity is directional.
- Here A is called the foreign key
- B is usually required to be the primary key or at least unique
- Multi-attribute foreign keys are allowed
- Given R.A -> S.B, potentially violating modifications are :
- Insert into R, delete from S, update R.A, update S.B
- So violations in the referencing table (R) are caught as errors by the DB. say R is Apply and B is Student/
- Now modifications in the referenced table B - constraint enforcement can be set up in different ways:
- Restrict : The deletion is not allowed in Student if some tuple in Apply is referencing it.
- Set null : Set the value of referencing tuple to null
- Cascade : If we delete a tuple, then delete all tuples that refer it.
- Above options work in the same way for update. Update to the referenced value will cause same updates in referencing value.
- If referential constraints are set up, then drop table of referencing table also wont be allowed.
- Example : For student update and college delete, the default constraint is restrict.
create table Apply(sID int references Student(ID) '''on delete set null''', cname text references College(cname) '''on update cascade''', major text, decision text).
- referential constraints can also be defined within the same table.
Triggers
- Monitor changes in the DB and when data is changed, they check conditions over the data and initiate actions
- A more "dynamic" concept
- Also known as "Event-Condition-Action-Rules" : When event occurs, check condition, if true: perform action
- e.g. if enrollment > 35000, then set all decision to "N", if applicant with GPA > 3.95 is inserted in the DB, then set decision to "Y".
- If size>7000, raise an error
- Original motivation for triggers was to move app logic into the DB.
- Why not write constraints instead of triggers ? In reality, expressing constraints is limited in DB's, but trigger features are quite expressive.
- Also constraints just raise errors, but trigger can fire an action that can fix the constraint violation.
create trigger name
Before | After | InsteadOf events
referencing variables
[For each row]
when (condition)
action
- events : <-- something like insert,delete, update on a table
- referencing variables <- reference the data that was modified when the trigger was activated (e.g. old row as var, new row as var, old table, new table). These vary depending on the event, for e.g. if event was insert only new data can be referred to. row level (for each row clause specified) : row and table vars can be referenced. Table refers to all the rows that were updated. statement level (for each clause not specificed): only table vars can be referenced.
- [For each row] <- execute trigger once for each row or just once overall
- Trigger is always activated at the end of the event statement.
- condition : SQL statement to be true for trigger to get executed.
- action : SQL statement to exec
- Trigger implementing referential integrity
create trigger cascade
after delete on S
referencing old row as O
for each row
delete from r where A = O.B
- Above written as statement level trigger
create trigger cascade
after delete on S
referencing old table as OT
delete from r where A in (select B from OT)
Examples
- Trigger for cascaded update - referential integrity
create trigger r3
after update of cName on college
for each row
begin
update apply
set cName = new.cName
where cName = old.cName
end
- Before event : trigger example.
- Maintain uniqueness of cname and raise an error if a duplicate cname is attempted to be inserted : raise(ignore) - raise and error, ignore the update : SQLite specific
create trigger r4
before insert of cName on college
for each row
when exists (select * from college where cname = New.cname)
begin
select raise(ignore)
end
- Self activating trigger (recursive trigger)
- This is actually infinite :
create trigger selftrig
after insert on T1
for each row
when (select count(*) from T1 < 10) //Terminating condition
begin
insert into T1 values (New.A + 1);
end
- Nested triggers immediately call each other
Views
- Physical - Disk; Conceptual - Relations
- Logical - Views (abstraction over Relations)
- View - query over relations
- Why views ? - Hide data from users; Make queries easier; Modularity of database access
- View V = ViewQuery(R1, R2, ... Rn)
- R can be a view as well.
- In reality a query over a view is rewritten by the DB to use the relations underneath.
- Create a view and use it as a regular table henceforth.
create view CSAccept as
select sid, cname
from apply
where major = 'cs' and decision = 'y'
Modifying Views
- Modifications to view are rewritten by the DB as modifications to the underlying table
- After the view modification, query on the view has to still hold. for e.g deleting a tuple from view - do the deletes on the underlying table, so that only that tuple is deleted from the view.
- Example, inserting element into view - how will the insert be done into base table ? Many different ways. Ambiguity has to be resolved.
- Rewriting process can be specified by view creator. But correctness guarantee not possible.
- Other approach is restrict view modifications to some operations only so that system can guarantee correctness.
View modification through triggers
- Rewriting process of views specified using triggers
create view csaccept as
select sid, cname
from apply
where major='cs' & decision='y'
- Deletion from view : delete from csaccept where sid = 123 : not allowed.
- So create a trigger that intercepts the delete & performs the underlying delete on the apply table
- Use instead of clause, also "old" var binds to the tuple the user wants to delete.
create trigger csacceptdelete
instead of delete on csaccept
for each row
begin
delete from apply
where sid = old.sid
and cname = old.cname
and major = 'cs' and decision = 'y'
end
- When a view includes aggregation, its a good idea not to modify it.
- Also when a view includes one col from the underlying relation or selects distinct values, insertions into view is not good. Because what would we insert for other columns ?
Automatic view modification
- SQL standard specifies updatable views. They have the following restrictions :
- select (no distinct) on a single table t
- Attributes not in view can be null or have default value
- Subqueries in view cannot view to the table t (but can refer to other table)
- No group by or aggregation in the view
- View modifications (inserts, updates) can be done normally and system automatically takes care of modifying the underlying base tables.
- However, take CSAccept view from above - we can do insert into CSAccept (333, 'Berkely'), but system will not insert anything meaningful in the underlying base table for major and decision & so we wont see it in the view either.
- we can add something called 'with check option' - which checks if the data actually gets added into the view
CREATE VIEW csaccept AS
SELECT sid, cname
FROM apply
WHERE major='cs' & decision='y'
with check option
Materialized Views
- Same advantages as regular views but additionally offer improved query performance.
- A physical table is actually created for a mat. view as opposed to just being a logical concept.
- However need to ensure mat. view stays in sync with modifications to underlying tables.
- Factors to create mat. views :
- Size of data
- Complexity of view
- Number of queries using view
- Number of modifications to base data that use the view
- The "query-update" trade off.
- Systems can use mat. views to rewrite queries automatically for perf. (like indexes)
Authorization
- Make sure users only see the data they are supposed to see
- Guard the database against modification by unauthorized users
- Users have privileges, can only on operate on data for which they are authorized.
- Select/Insert/Update/Delete permissions with specific attributes enabled
- Suppose we want to give access to users to access only info relating to "Stanford" in applications db, then we can do that by creating a stanford specific view. Then grant users privileges on that view.
- Authorization is one of the most imp. uses for views.
- By default table creator is owner and can grant privileges to other users.
grant privs on R to users
[with grant options]
- Grant options can be specified to allow other users to grant
- Revoke privileges - comes with cascade or restrict options. Cascade will revoke privileges recursively. Restrict will not.
Recursion
- SQL couldnt perform unbounded computations.
- e.g. Parentof(parent, child) - find all ancestors of child. grandparents - 1 self-join, higher up - more joins - but no of joins cant be dynamic.
- "With" construct was added to introduce recursion to SQL.
with recursive R1 as (query-1)
R2 as (query-2)
Rn as (query-n)
<query involving R1,..Rn>
- R1..Rn are relations that dont actually exist in the Database and will contain the results of query-1..query-n.
- Recursive keyword is for recursive queries, query-1 can refer to R1 itself.
- Recursive keyword is for recursive queries, query-1 can refer to R1 itself.
with recursive
R as (base query)
UNION
(recursive query)
<query involving R and other tables>
- Base query doesnt depend on R, recursive query depends on R and final query is run when the recursion terminates.
OLAP
- DB activity in two broad classes:
- OLTP : Short transactions - queries/updates, touch small portions of data, frequent updates to data.
- OLAP : Long transactions, complex queries, large portions of data, infrequent updates to data.
- Data warehousing : Software architecture that brings data from different OLTP sources into a single "warehouse" for OLAP analysis.
- DSS : Infrastructure for data analysis. e.g. data warehouse tuned for OLAP.
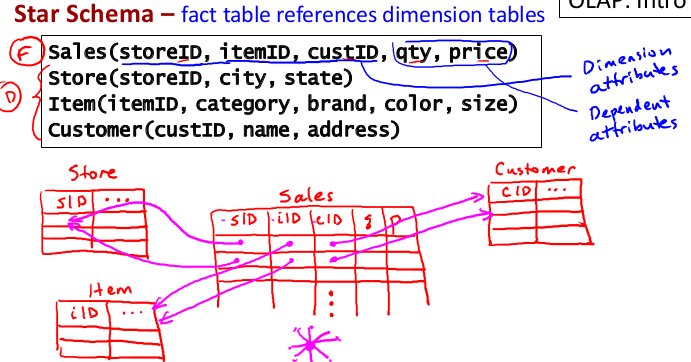
- Star Schema :
- Fact table : Usually one such table. Updated frequently, often append-only (only inserts) and very large in size. e.g sales transactions, course enrollments, page views.
- Dimension tables : Many such tables. Updated infrequently, but not as large. e.g. stores, items, customers, students, courses, web pages, users, advertisers.
- Analogy : Dimension tables are things in the real world and fact tables are logging things that happened.
- Fact tables reference dimension tables in a star schema :
- OLAP queries usually follow the pattern : Join -> Filter -> Group -> Aggregate
- Perf. for these kind of queries tends to be slow. But special indexes and query processing techniques can handle.
- Materialized views : Useful for perf. when large queries and not many updates.
- Data Cubes :
- Different way of looking at data in star schema.
- Dimension data forms the axes of "cube".
- Fact data in cells - the inside of the cube. e.g. one cell will contain the dependent attributes - quantity, price for every combo of item, customer and store.
- Aggregated data on sides, edges and corner. e.g. one side may contain sum of sales for customer and stores (for a item), another side will contain sum of sales for items and stores (for a particular customer) etc.
- Corner contains aggregated data on the whole cube.
OLAP Queries
- Star join :
select *
from Sales F, Store S, Item I, Customer C
where F.storeID = S.storeID and F.itemID = I.itemID and F.custID = C.custID;
- Grouping and aggregation over fact table : Total sales by store and customer. Typical OLAP Query
select storeID, custID, sum(price)
from Sales
group by storeID, custID;
- Drill down : If more details are required. e.g. in the above query add item to the select and group by clause to get item details.
- Slicing : Analyze a slice of the data cube.
select F.storeID, itemID, custID, sum(price)
from Sales F, Store S
where F.storeID = S.storeID
and state = 'WA'
group by F.storeID, itemID, custID;
- Dice : Slice the data cube in two dimensions to give a chunk of the cube
select F.storeID, I.itemID, custID, sum(price)
from Sales F, Store S, Item I
where F.storeID = S.storeID and F.itemID = I.itemID
and state = 'WA' and color = 'red'
group by F.storeID, I.itemID, custID;
- Rolling up : Want to have less detail (more aggregation), take out attributes from group by clause.
- SQL constructs added to support OLAP are "with cube" and "with rollup". These are added to the group by clause.
- WITH CUBE : Adds faces, edges, and corners of data cube : sum of price for a given item, customer across all stores, sum of price for a store for all items etc.
- Internal data of the cube : no group by, faces, edges and corners : represent the group by portion.
select storeID, itemID, custID, sum(price)
from Sales
group by storeID, itemID, custID with cube;
- OLAP app's need to query the cube directly. Create the cube using a mat. view or as a separate table.
create table Cube as
select storeID, itemID, custID, sum(price) as p
from Sales
group by storeID, itemID, custID with rollup
union
select storeID, itemID, custID, sum(price) as p
from Sales
group by itemID, custID, storeID with rollup
union
select storeID, itemID, custID, sum(price) as p
from Sales
group by custID, storeID, itemID with rollup;
- Running queries directly on the cube table :
- Cust is null - that is we want data that is preaggregated for all the customers - on the face of the cube.
- IF we use is not null, then we'll get the data per customer -we move into the innards of the cube.
select C.*
from Cube C, Store S, Item I
where C.storeID = S.storeID and C.itemID = I.itemID
and state = 'CA' and color = 'blue' and custID is null;
- Using the summarized data from the cube can be orders of magnitude faster that querying the fact data.
- With rollup : Makes sense for hierarchical dimensions. e.g state, county, city : all combo's of state, county,city wont occur since only some combos are valid.
- So will rollup in the group by clause order. With cube will do it for all combos - but not all will be meaningful. e.g. we dont all combo's of State and BLR, since BLR occurs in only one state.
select state, county, city, sum(price)
from Sales F, Store S
where F.storeID = S.storeID
group by state, county, city with rollup;